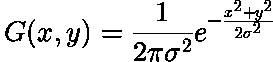Classical Computer Vision Basics

• Image representation
• Convolutional filters
• Thresholding
• Morphological operations
  • erosion, dilation, etc.
• Instance segmentation
  • connected components
  • watershed
• Object analysis

What is Computer Vision?

• Computer Vision: "is an interdisciplinary scientific field that deals with how computers can gain high-level understanding from digital images or videos."
• Related field: signal processing: processing of (1d) digital signals
  • many approaches can be extended to 2d (images) or higher d
• More general: also analysis of image series
  • over time: videos
  • over space: volumetric imaging (e.g. LIDAR, microscopy, medical imaging (CT-scans))

# Important python libraries:

import numpy as np  # we always need numpy
import scipy.ndimage  # image processing module in scipy
import matplotlib.pyplot as plt  # for displaying images

import imageio  # reading and writing images 
import skimage  # computer vision library
# import opencv  <- also very popular, but harder to use

Image representation

• "Natural images": images of the natural world
• digital images are taken by digital camera (e.g. CCD)
• 2 image dimensions, 1 channel dimension (color space):
• H x W x C
• C = 3 (because of how we perceive color)

RGB representation

• Image has 3 color channels -> 3d "tensor"
• Dim 0, 1 = image dimensions, dim 2 = color channel

# look at an example rgb image
image = skimage.data.astronaut()
print(image.shape)
print(image.dtype, image.min(), image.max())

(512, 512, 3)
uint8 0 255

fig, ax = plt.subplots(1, figsize=(8, 8))
ax.imshow(image)
ax.axis("off")
plt.show()

Other representations

RGB is not the only way to represent color space. Examples:

• CMYK: used for printing, because it's better applicable to ink mixing
• YUV: used for image compression
• HSV: Hue Saturation Value: used by artists, more natural to think about

https://en.wikipedia.org/wiki/Color_space#Generic

# convert image to hsv and increase the saturation
image_hsv = skimage.color.rgb2hsv(image)
image_hsv[..., 1] = np.clip(image_hsv[..., 1] * 5, 0, 255)

more_saturation = skimage.color.hsv2rgb(image_hsv)

fig, ax = plt.subplots(1, 2, figsize=(8, 4))
ax[0].imshow(image)
ax[0].axis("off")
ax[1].imshow(more_saturation)
ax[1].axis("off")
plt.show()

Clipping input data to the valid range for imshow with RGB data ([0..1] for floats or [0..255] for integers).

Image data formats & compression

• JPEG: lossy compression based on discrete fourier transform and discarding high frequency
• PNG: lossless compression using gzip
• TIFF: more complex format that supports multiple images and volumetric data
• MPEG: video format including lossy video compression

(also: vector graphics, e.g. svg)

• https://en.wikipedia.org/wiki/JPEG
• https://en.wikipedia.org/wiki/TIFF
• https://en.wikipedia.org/wiki/Portable_Network_Graphics
• https://en.wikipedia.org/wiki/Moving_Picture_Experts_Group

Scientific images

• 3 channels (C=3) is specific to natural images (because of our perceptual color space)
• scientific images often just contain only single channel and are displayed as grayscale
  • similar to old black & white fotos
• but can also contain more channels, e.g.
  • multiple spectra in astronomy
  • multiple fluorescent dies in microscopy

# load image of nuclei for normal and apoptotic cells
# (apoptose = programmed cell death)
url = "https://s3.embl.de/ilastik-downloads/2d_cells_apoptotic_1channel.png"
image = imageio.imread(url)
print(image.shape)

(1024, 1344)

fig, ax = plt.subplots(1, figsize=(12, 12))
ax.imshow(image, cmap="gray")
ax.axis("off")
plt.show()

Convolutional filters

• Kernel approximation of functions that are convolved with image.
• Can implement smoothing, edge detectors, texture detectors, etc.

Difference to CNNs:

• "classical" convolutional filters: fixed kernel, e.g. to smooth the image
• CNN: composition of many learned kernels

Smoothing: Gaussian Blur

Convolve image with a gaussian kernel:

Profile for sigma=1

https://homepages.inf.ed.ac.uk/rbf/HIPR2/gsmooth.htm

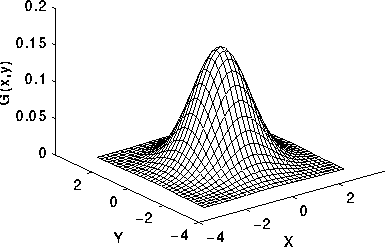
In practice: finite kernel approximation: (sigma=1)

https://homepages.inf.ed.ac.uk/rbf/HIPR2/gsmooth.htm

Convolution: Sliding window

Kernel is applied to the image as sliding window

# apply gaussian blur with 2 different sigma values
smoothed1 = skimage.filters.gaussian(image, 2)
smoothed2 = skimage.filters.gaussian(image, 8)
fig, ax = plt.subplots(1, 3, figsize=(16, 8))
ax[0].imshow(image, cmap="gray")
ax[0].axis("off")
ax[1].imshow(smoothed1, cmap="gray")
ax[1].axis("off")
ax[2].imshow(smoothed2, cmap="gray")
ax[2].axis("off")
plt.show()

Edge filter: Laplacian

Find edges in image using "Laplacian" filter (second spatial derivative):

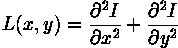
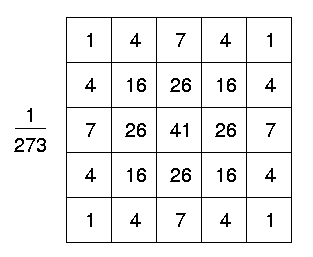
Kernel approximations:

https://homepages.inf.ed.ac.uk/rbf/HIPR2/log.htm

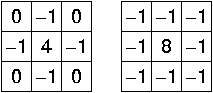
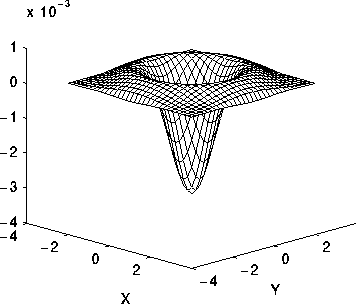
Problem: sensitive to noise => Apply gaussian smoothing first: Laplacian of Gaussian

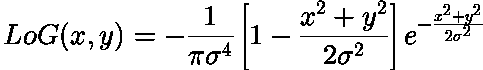
Profile of the Laplacian of Gaussian

https://homepages.inf.ed.ac.uk/rbf/HIPR2/log.htm

# apply laplacian of gaussian filter to find edges
edges = skimage.filters.laplace(smoothed1)
fig, ax = plt.subplots(1, 2, figsize=(16, 8))
ax[0].imshow(image, cmap="gray")
ax[0].axis("off")
ax[1].imshow(edges, cmap="gray")
ax[1].axis("off")
plt.show()

More convolutional filters

• Difference of Gaussians: subtract two gaussians with different sigma -> edge filter
• Hessian Eigenvalues: eigenvalues of the matrix of sencond partial spatial derivatives -> texture filter
• Structure Tensor: measures gradient distribution -> texture filter

Thresholding

For analysis: segment image into different components (Semantic Segmentation)

simplest approach: foreground background segmentation through thresholding (Binary Segmentation)

Threshold can be derived from image intensity histogram

Advanced thresholding:

• Otsu's method to find threshold that separates foreground and background https://en.wikipedia.org/wiki/Otsu%27s_method
• Adaptive thresholding: find best threshold for local patch instead of one global threshold

# plot histogram of the image
fig, ax = plt.subplots(1, figsize=(8, 8))
histo = ax.hist(image.ravel())
plt.show()

# good threshold from histogram: 25-50
threshold = 50
# apply the threshold
thresholded = image > threshold
print("Values in thresholded image:", np.unique(thresholded))

fig, ax = plt.subplots(1, 2, figsize=(16, 8))
ax[0].imshow(image, cmap="gray")
ax[0].axis("off")
ax[1].imshow(thresholded)
ax[1].axis("off")
plt.show()

Values in thresholded image: [False  True]

Morphological operations

Apply small structure element to image:

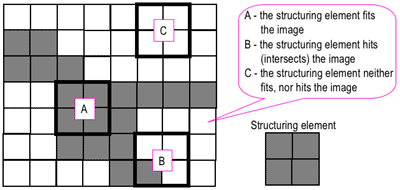
https://www.cs.auckland.ac.nz/courses/compsci773s1c/lectures/ImageProcessing-html/topic4.htm

Erosion: Output is 1 if structure element fits the image -> shrinks the image

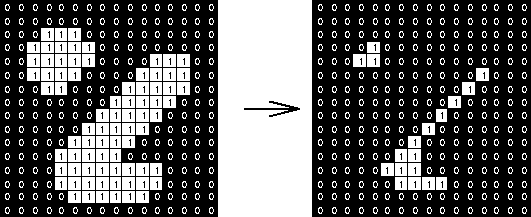
Dilation: Output is 1 if structure element hits the image grows the image

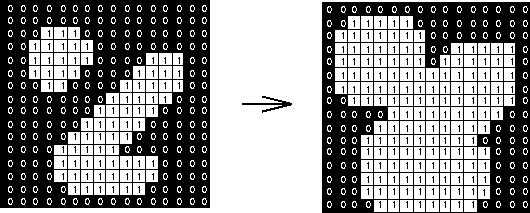
https://www.cs.auckland.ac.nz/courses/compsci773s1c/lectures/ImageProcessing-html/topic4.htm

More complex morphological operations:

• opening: erosion followed by dilation: gets rid of small structures, large structures stay the same
• closing: dilation followed by erosion: fills holess

# apply erosion and dilation to our binary mask
eroded = scipy.ndimage.morphology.binary_erosion(thresholded, iterations=4)
dilated = scipy.ndimage.morphology.binary_dilation(thresholded, iterations=4)

fig, ax = plt.subplots(1, 3, figsize=(16, 16))
ax[0].imshow(thresholded)
ax[0].axis("off")
ax[1].imshow(eroded)
ax[1].axis("off")
ax[2].imshow(dilated)
ax[2].axis("off")
plt.show()

Instance Segmentation

Label each object in the image (and its pixels) with a unique id

• semantic segmentation:
  • number of label values is known a priori (number of classes is known)
• instance segmentation:
  • number of label values is not known a priori (number of objects is unknown)

Connected components

Label pixels that are connected in the image as one component Depends on the definition of neighborhood (i.e. connected or not)

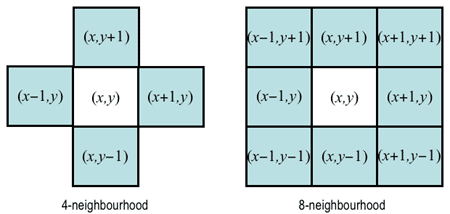
https://www.cs.auckland.ac.nz/courses/compsci773s1c/lectures/ImageProcessing-html/topic3.htm#connect

Connected component labeling:

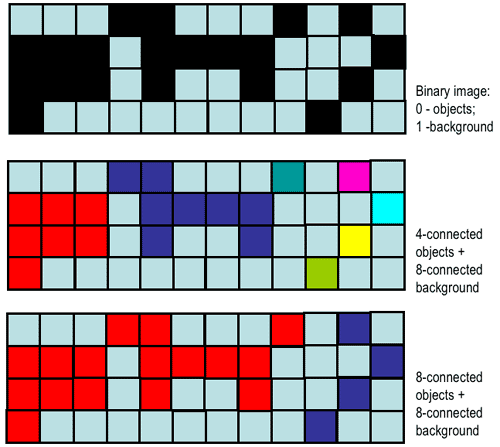
https://www.cs.auckland.ac.nz/courses/compsci773s1c/lectures/ImageProcessing-html/topic3.htm#connect

Connected Components Algorithm:

• uses Union Find Datastructure
• 2 Passes:
  • first pass: find which pixels are connected
  • second pass: assign to each pixel the label value of its component

# apply connected components to the foreground/background segmentation
components = skimage.measure.label(thresholded)
print("Number of components:", len(np.unique(components)))

Number of components: 227

# this is finding a good color map for the components image
from matplotlib import colors
n_components = len(np.unique(components)) - 1
random_colors = [[0, 0, 0]] + np.random.rand(n_components, 3).tolist()
random_colors = colors.ListedColormap(random_colors)

# display the connected components using random colors (code not shown)
fig, ax = plt.subplots(1, 2, figsize=(16, 16))
ax[0].imshow(image, cmap="gray")
ax[0].axis("off")
ax[1].imshow(components, cmap=random_colors, interpolation="nearest")
ax[1].axis("off")
plt.show()

Watershed

Interpret image as height map; "flood" with water, watersheds correspond to object boundaries

Different perspective: Seeded watershed: grow regions starting from seeds:

Finding seeds:

• use local minima of height map
• or: use external markers

# find seeds, height map and mask for the watershed

# seeds: components of strong eroded threshold image
seeds = skimage.measure.label(
    scipy.ndimage.binary_erosion(thresholded, iterations=8)
)

# height map: the edge filter
hmap = edges

# mask: the thresholded image
mask = thresholded

nuclei = skimage.segmentation.watershed(hmap, markers=seeds, mask=mask)
n_nuclei = len(np.unique(nuclei)) - 1
print("Number of segmented nuclei:", n_nuclei)

Number of segmented nuclei: 95

random_colors = [[0, 0, 0]] + np.random.rand(n_nuclei, 3).tolist()
random_colors = colors.ListedColormap(random_colors)

fig, ax = plt.subplots(1, 2, figsize=(16, 16))
ax[0].imshow(image, cmap="gray")
ax[0].axis("off")
ax[1].imshow(nuclei, cmap=random_colors, interpolation="nearest")
ax[1].axis("off")
plt.show()

Object analysis

Instance segmentation often is the basis for further object based analysis, e.g.

• count objects
• analyze spatial distribution
• compare morphology of the objects
• ...

Here: distinguish nuclei into normal and apoptotic based on mean object intensity

# compute the mean intensities per nucleus
nucleus_properties = skimage.measure.regionprops(nuclei, image)
mean_intensities = np.array([prop.mean_intensity for prop in nucleus_properties])

# look at the intensity histogram
h = plt.hist(mean_intensities)

apoptotic_threshold = 80
apoptotic_nuclei = np.where(mean_intensities >= 80)[0] + 1
normal_nuclei = np.where(mean_intensities < 80)[0] + 1
print("Nr normal nuclei:", len(normal_nuclei))
print("Nr apo nuclei:", len(apoptotic_nuclei))

Nr normal nuclei: 44
Nr apo nuclei: 51

classified_nuclei = np.zeros_like(image)
classified_nuclei[np.isin(nuclei, normal_nuclei)] = 1
classified_nuclei[np.isin(nuclei, apoptotic_nuclei)] = 2

# display the classified cells as image
cmap = colors.ListedColormap(["white", "blue", "yellow"])
fix, ax = plt.subplots(1, 2, figsize=(20, 10))
ax[0].imshow(image, cmap="gray")
ax[0].axis("off")
ax[0].set_title("Image")
ax[1].imshow(classified_nuclei, cmap=cmap, interpolation="nearest")
ax[1].set_title("Classified cells")
ax[1].axis("off")

(-0.5, 1343.5, 1023.5, -0.5)

# we arrived back at a semantic segmnentation!